Development of a reduced estimator to estimate the variance and covariance matrix with large dimensions using hyperbolic trigonometric functions - (Chemical properties of the soil of the Tigris Basin in Wasit Governorate)
Keywords:
covariance matrix using hyperbolic trigonometric functions, Large-dimensional varianceAbstract
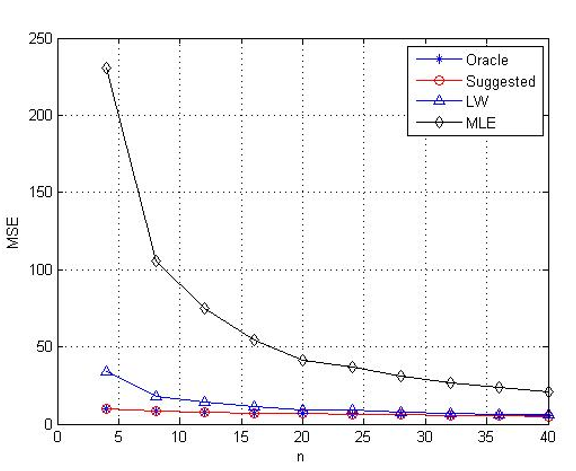
When the dimensions of the covariance matrix are relatively large compared with the sample size ; or when the dimensions of the matrix are close to the sample size or larger, There will be difficulties in finding a good estimation for it. Most Matrices with high dimension suffer from the difficulty of finding their inverse. Therefore, the classical methods of estimation such as maximum likelihood will give biased estimators and far from their true value. This research aims at expanding usage of shrinkage estimation to estimate the covariance matrix in the case of using samples with large dimensions.The covariance matrix will be estimated by using three methods. The Maximum Likelihood estimator MLE and the nonlinear shrinkage estimator Oracle, and the linear shrinkage estimator Lediot and Wolf (LW) and the Suggested Estimator and make comparison among them based on (MMSE) minimum mean square errors. Here, a simulated experiment with high dimensions samples was made with multiple sizes and calculated MMSE as the increasing in sample size to the large dimension of covariance matrix.
As conclusions, the Suggested Estimator is perfect when the sample size is very small compared with the number of variables in it. Moreover, the Oracle estimator is working well when the sample size is fairly small to the number of variables in it while it has not cleared that the maximum likelihood estimator MLE and the (LW) have any goodness.
References
. CHEN, Y., WIESEL, A. and HEREO, A. O. (2011). Robust
shrinkage estimation of high dimensional covariance matrices. IEEE
Transactions on Signal Processing, vol. 59, issue. 9.
. CHEN, Y. A., WIESEL, A. and ELDAR, A. O. (2010).
Shrinkage Algorithms for MMSE covariance estimation.
IEEE Transactions on Signal Processing, vol. 58, issue 10.
. DEY, D. K. and SRINIVASAN, C. (1985). Estimation of a
covariance matrix under Stien's loss. The Annals of Statistics, vol. 13,
No. 4, pp. 1581-1591.
. FISHER, T. J. and SUN, X. (2011). Improved Stein-type
shrinkage estimator for the high-dimensional multivariate normal
covariance matrix. Comp. Statist. Data Analysis, 55, 1909-1918.
. FROST, P. A. and SAVARINO, J. E. (1986). An empirical Bayes
Approach to Portfolio selection. Journal of Financial and Quantitate
Analysis, 21: 293- 305
. FUJIKOSHI, Y., ULYANOV, V. and SHIMIZU, R. (2011).
Multivariate Statistics: High-Dimensional and Large-Sample
Approximations. Wiley Series in Probability and Statistics.
. HAFF, L. (1980). Empirical Bayes estimation of the multivariate
normal covariance matrix," The Annals of Statistics, vol. 8, no. 3,
pp. 586-597.
. HOREL, A. E. and KENNARD, R. W. (1970). Ridge regression;
biased estimation for nonorthogonal problems. Technometrics,
vol. 12, pp. 55-82.
. HORVATH, Z. and JOHNSTONE, R. (2000). AR(1) Time series
process. Econometrics 7590, Utah University Press.
. JOHNSTONE, I. M. and TITTERINGTON, D. M. (2009).
Statistical Challenges of high-dimensional data. Philosophical
Transactions of the Royal Society. 367, pp. 4237-4253.
. KINCAID, C. (2005). Guidelines for selection the covariance
structure in mixed model analysis. Proceedings of the 30th annual
SAS, Paper 198-30.
. LEDOIT, O. and WOLF, M. (2004). A well-conditioned
estimator for large- dimensional covariance matrices, Journal of
Multivariate Analysis, vol. 88, no.2, pp. 365-411.
. LEDOIT, O. and WOLF, M. (2012). Nonlinear shrinkage
estimation of large-dimensional covariance matrices. The Annals of
Statistics. Vol. 40, No. 2, pp. 1024–1060.
. MARTINEZ, W. L. and MARTINEZ, A. R. (2002).
Computational Statistics Handbook with MATLAB,
Chapman & Hall/CRC Press.
. SRIVASTAVA, M. S. (2005). Some tests concerning the covariance
matrix in high dimensional data. J. Japan Statist. Soc. 35(2), 251-272.
. STIEN, C., EFRON, B. and MORRIS, C. (1972). Improving the
usual estimator of a normal covariance matrix, National Science
Foundation Grant, Technical Report, No. 37.
. ZWILLINGER, D. (2012). Standard Mathematical Tables and Formulae.
ed. CRC Press. Taylor & Francis Groups. NW. USA
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2017 Iraqi Journal for Administrative Sciences

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Authors retain the copyright of their papers without restrictions.



