تطوير مقدر مقلص لتقدير مصفوفة التباين والتباين المشترك ذات الابعاد الكبيرة باستخدام الدوال المثلثية الزائدية ( الخصائص الكيميائية لتربة حوض دجلة في محافظة واسط)
الكلمات المفتاحية:
مصفوفة التباين والتباين المشترك ذات الابعاد الكبيرة باستخدام، الدوال المثلثية الزائديةالملخص
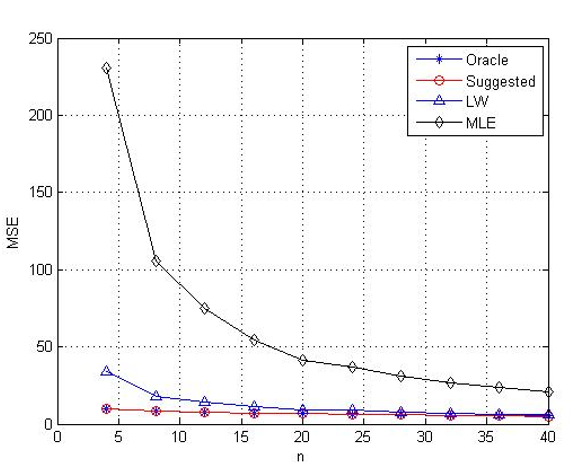
عندما تكون ابعاد مصفوفة التباين والتباين المشترك كبيرة بالنسبة الى حجم العينة اي ان المصفوفة ذات ابعاد تكون قريبة الى حجم العينة او أكبر منها. ستكون هناك صعوبات في ايجاد تقدير جيد لها اذ ان اغلب المصفوفات بتلك الابعاد ستعاني من صعوبة ايجاد المعكوس لهذه المصفوفات. لذلك فان طرق التقدير التقليدية مثل طريقة الامكان الاعظم ستعطي تقديرات متحيزة ويكون التقدير بعيدا عن قيمته الحقيقية. يهدف البحث الى التوسع في استعمال لمقدرات المقلصة لتقدير مصفوفة التباين والتباين المشترك في حالة استعمال عينات ذات ابعاد كبيرة. وهنا سيتم تقدير تلك المصفوفة باستعمال ثلاث طرق والمقارنة فيما بينها بالاعتماد على أصغر مربعات خطاء. تم استعمال مقدر الإمكان الأعظم MLE وكذلك مقدر غير خطي وهو مقدر الاوراكل Oracle Estimator وكذلك مقدر مقلص خطي وهو Lediot and Wolf Estimator LW والمقدر المقترح من لدن الباحث واجرينا محاكاة لأحجام عينات مختلفة وبأبعاد كبيرة وحساب أصغر مربعات خطاء عند ازدياد حجم العينة بالنسبة الى ابعاد مصفوفة التباين والتباين المشترك
وتوصل الباحث الى ان المقدر المقترح يكون الافضل عندما يكون حجم العينة صغيراً بالنسبة الى عدد المتغيرات فيها وكذلك ان مقدر الاوراكل يعمل جيدا عندما يكون حجم العينة صغيرا نوعا ما الى عدد المتغيرات فيها بينما لم تتوضح اية افضلية لمقدر الإمكان الأعظم وكذلك مقدر LW.
المراجع
. CHEN, Y., WIESEL, A. and HEREO, A. O. (2011). Robust
shrinkage estimation of high dimensional covariance matrices. IEEE
Transactions on Signal Processing, vol. 59, issue. 9.
. CHEN, Y. A., WIESEL, A. and ELDAR, A. O. (2010).
Shrinkage Algorithms for MMSE covariance estimation.
IEEE Transactions on Signal Processing, vol. 58, issue 10.
. DEY, D. K. and SRINIVASAN, C. (1985). Estimation of a
covariance matrix under Stien's loss. The Annals of Statistics, vol. 13,
No. 4, pp. 1581-1591.
. FISHER, T. J. and SUN, X. (2011). Improved Stein-type
shrinkage estimator for the high-dimensional multivariate normal
covariance matrix. Comp. Statist. Data Analysis, 55, 1909-1918.
. FROST, P. A. and SAVARINO, J. E. (1986). An empirical Bayes
Approach to Portfolio selection. Journal of Financial and Quantitate
Analysis, 21: 293- 305
. FUJIKOSHI, Y., ULYANOV, V. and SHIMIZU, R. (2011).
Multivariate Statistics: High-Dimensional and Large-Sample
Approximations. Wiley Series in Probability and Statistics.
. HAFF, L. (1980). Empirical Bayes estimation of the multivariate
normal covariance matrix," The Annals of Statistics, vol. 8, no. 3,
pp. 586-597.
. HOREL, A. E. and KENNARD, R. W. (1970). Ridge regression;
biased estimation for nonorthogonal problems. Technometrics,
vol. 12, pp. 55-82.
. HORVATH, Z. and JOHNSTONE, R. (2000). AR(1) Time series
process. Econometrics 7590, Utah University Press.
. JOHNSTONE, I. M. and TITTERINGTON, D. M. (2009).
Statistical Challenges of high-dimensional data. Philosophical
Transactions of the Royal Society. 367, pp. 4237-4253.
. KINCAID, C. (2005). Guidelines for selection the covariance
structure in mixed model analysis. Proceedings of the 30th annual
SAS, Paper 198-30.
. LEDOIT, O. and WOLF, M. (2004). A well-conditioned
estimator for large- dimensional covariance matrices, Journal of
Multivariate Analysis, vol. 88, no.2, pp. 365-411.
. LEDOIT, O. and WOLF, M. (2012). Nonlinear shrinkage
estimation of large-dimensional covariance matrices. The Annals of
Statistics. Vol. 40, No. 2, pp. 1024–1060.
. MARTINEZ, W. L. and MARTINEZ, A. R. (2002).
Computational Statistics Handbook with MATLAB,
Chapman & Hall/CRC Press.
. SRIVASTAVA, M. S. (2005). Some tests concerning the covariance
matrix in high dimensional data. J. Japan Statist. Soc. 35(2), 251-272.
. STIEN, C., EFRON, B. and MORRIS, C. (1972). Improving the
usual estimator of a normal covariance matrix, National Science
Foundation Grant, Technical Report, No. 37.
. ZWILLINGER, D. (2012). Standard Mathematical Tables and Formulae.
ed. CRC Press. Taylor & Francis Groups. NW. USA
التنزيلات
منشور
كيفية الاقتباس
إصدار
القسم
الرخصة
الحقوق الفكرية (c) 2017 https://creativecommons.org/licenses/by-nc-nd/4.0/

هذا العمل مرخص بموجب Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
يحتفظ المؤلفون بحقوق الطبع والنشر لأوراقهم دون قيود.



